soal 2004
| 1. |
Persamaan kuadrat yang akar-akarnya 5 dan -2 adalah ........ |
| |
|
| 2. |
Suatu peluru ditembakkan ke atas. Tinggi peluru pada t detik dirumuskan oleh h(t) = 40t - 5t² (dalam meter). Tinggi maksimum yang dapat ditempuh oleh peluru tersebut adalah ........ |
| |
|
| 3. |
Pada segitiga ABC diketahui sisi AB = 6 cm, AC =10 cm, dan sudut A = 60°. Panjang sisi BC = ........ |
| |
|
| 4. |
Nilai sin 45° cos 15° + cos 45° sin 15° sama dengan ........ |
| |
|
| 5. |
Persamaan fungsi grafik di bawah ini adalah ........
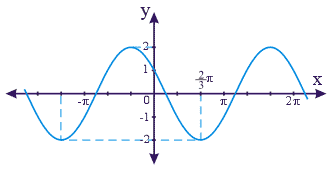 |
| |
|
| 6. |
Penyelesaian persamaan sin (x - 45°) > 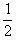 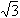 untuk 0 untuk 0 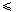 x x 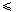 360 adalah ........ 360 adalah ........ |
| |
|
| 7. |
Himpunan penyelesaian persamaan 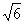 sin x° + sin x° + 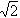 cos x° = 2 untuk 0 cos x° = 2 untuk 0 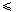 x < 360 adalah ........ x < 360 adalah ........ |
| |
|
| 8. |
Jika log 2 = 0,301 dan log 3 = 0,477, maka log 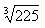 = ........ = ........ |
| |
|
| 9. |
Himpunan penyelesaian persamaan : 93x - 2 . 33x + 1 - 27 = 0 adalah ........ |
| |
|
| 10. |
Himpunan penyelesaian pertidaksamaan : 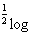 (x2 - (x2 -  < 0 adalah ........ < 0 adalah ........ |
| |
|
| 11. |
Himpunan penyelesaian sistem persamaan :
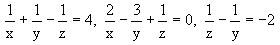 adalah ........ adalah ........ |
| |
|
| 12. |
Diketahui matriks S = 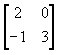 dan M = dan M = 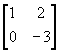 jika fungsi f(S,M) = S² - M², maka matriks f(S+M, S-M) adalah ........ jika fungsi f(S,M) = S² - M², maka matriks f(S+M, S-M) adalah ........ |
| |
|
| 13. |
Nilai 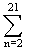 (5n - 6) = ........ (5n - 6) = ........ |
| |
|
| 14. |
Data yang diperoleh dari hasil pengamatan setiap hari terhadap tinggi sebuah tanaman membentuk barisan geometri. Bila pada pengamatan hari kedua adalah 2 cm dan pada hari keempat adalah 3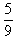 cm, maka tinggi tanaman tersebut pada hari pertama pengamatan adalah ........ cm, maka tinggi tanaman tersebut pada hari pertama pengamatan adalah ........ |
| |
|
| 15. |
Dua dadu dilambungkan bersama-sama. Peluang muncul mata dadu pertama 3 dan mata dadu kedua 5 adalah ........ |
| |
|
| 16. |
Modus dari data pada gambar di bawah ini adalah ........
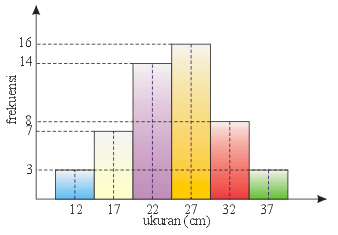 |
| |
|
| 17. |
Suatu pemetaan f : R 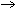 R, g : R R, g : R 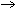 R dengan (g R dengan (g 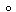 f) (x) = 2x² + 4x + 5 dan g(x) = 2x + 3, maka f(x) = ........ f) (x) = 2x² + 4x + 5 dan g(x) = 2x + 3, maka f(x) = ........ |
| |
|
| 18. |
Nilai 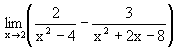 = ........ = ........ |
| |
|
| 19. |
Nilai 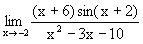 = ........ = ........ |
| |
|
| 20. |
Turunan pertama dari fungsi f(x) = 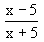 adalah ........ adalah ........ |
| |
|
| 21. |
Turunan pertama dari y = cos²(2x -  ),adalah ........ ),adalah ........ |
| |
|
| 22. |
Dengan persediaan kain polos 20 m dan kain bergaris 10 m, seorang penjahit akan membuat 2 model pakaian jadi. Model I memerlukan 1 m kain polos dan 1,5 m kain bergaris. Model II memerlukan 2 m kain polos dan 0,5 m kain bergaris. Bila pakaian tersebut dijual, setiap model I memperoleh untung Rp 15.000,00 dan model II memperoleh untung Rp 10.000,00. Laba maksimum yang diperoleh adalah sebanyak ....... |
| |
|
| 23. |
Jika vektor 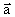 = = 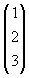 , , 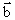 = = 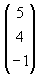 , dan , dan 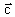 = = 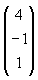 , maka vektor , maka vektor 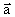 + 2 + 2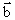 - 3 - 3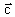 sama dengan ........ sama dengan ........ |
| |
|
| 24. |
Diketahui vektor 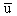 = = 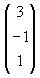 dan vektor dan vektor  = = 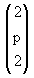 . Jika proyeksi skalar ortogonal vektor . Jika proyeksi skalar ortogonal vektor 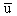 pada arah vektor pada arah vektor  sama dengan setengah panjang vektor sama dengan setengah panjang vektor  , maka nilai p adalah ........ , maka nilai p adalah ........ |
| |
|
| 25. |
Persamaan garis singgung pada lingkaran x² + y² - 2x + 4y - 4 = 0 yang tegak lurus garis 5x -12y + 15 = 0 adalah ........ |
| |
|
| 26. |
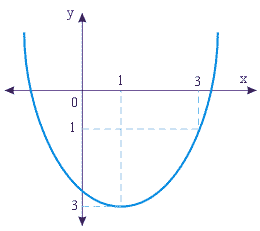
Persamaan parabola pada gambar di atas adalah ........ |
| |
|
| 27. |
Persamaan elips dengan fokus (2, 1) dan (8, 1) serta panjang sumbu mayor 10 adalah........ |
| |
|
| 28. |
Titik potong sumbu x dengan salah satu asimptot hiperbola :
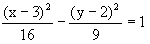 adalah ........ adalah ........ |
| |
|
| 29. |
Suku banyak (x4 - 3x3 - 5x2 + x - 6) dibagi oleh (x2 - x - 2), sisanya sama dengan ........ |
| |
|
| 30. |
Gradien garis singgung di sembarang titik pada suatu kurva ditentukan oleh rumus y' = 3x2 - 6x + 2. Jika kurva tersebut melalui titik (1, -5), maka persamaan kurvanya adalah ........ |
| |
|
| 31. |
Luas daerah pada kuadran I yang dibatasi oleh kurva y = x² - 2x - 3,
garis 5x - 3y - 5 = 0, dan sumbu x adalah ........ |
| |
|
| 32. |
Nilai dari 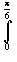 4 sin 7x cos 3x dx = ........ 4 sin 7x cos 3x dx = ........ |
| |
|
| 33. |
Hasil dari 16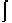 (x + 3) cos (2x - (x + 3) cos (2x -  ) dx = ........ ) dx = ........ |
| |
|
| 34. |
T1 adalah transformasi rotasi pusat O dan sudut putar 90°. T2 adalah transformasi pencerminan terhadap garis y = -x. Bila koordinat peta titik A oleh transformasi T1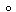 T2 adalah A'(8, -6), maka koordinat titik A adalah ........ T2 adalah A'(8, -6), maka koordinat titik A adalah ........ |
| |
|
| 35. |
Persamaan peta kurva y = x² - 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasi dengan pusat O dan faktor Skala 3 adalah ........ |
| |
|
| 36. |
Diketahui kubus ABCD.EFGH dengan panjang rusuk 12 cm. K adalah titik tengah rusuk AD. Jarak titik K ke garis HC adalah ........ |
| |
|
| 37. |
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Panjang proyeksi DE pada bidang BDHF adalah ........ |
| |
|
| 38. |
Pada limas segiempat beraturan T.ABCD yang semua rusuknya sama panjang. Sudut antara TA dan bidang ABCD adalah ........ |
| |
|
| 39. |
Ingkaran dari pernyataan "Semua makhluk hidup perlu makan dan minum."adalah ........ |
| |
|
| 40. |
Diberikan pernyataan-pernyataan sebagai berikut :
1. Jika penguasaan matematika rendah, makin sulit untuk menguasai IPA.
2. IPA tidak sulit dikuasai atau IPTEK tidak berkembang.
3. Jika IPTEK tidak berkembang, maka negara akan semakin tertinggal.
Dari ketiga pernyataan di atas dapat disimpulkan ........ |
| |
|
kunci:
|
|
|
1.
|
E
|
|
2.
|
B
|
|
3.
|
A
|
|
4.
|
C
|
|
5.
|
C
|
|
6.
|
C
|
|
7.
|
A
|
|
8.
|
E
|
|
9.
|
A
|
|
10.
|
C
|
|
11.
|
C
|
|
12.
|
A
|
|
13.
|
B
|
|
14.
|
C
|
|
15.
|
E
|
|
16.
|
A
|
|
17.
|
A
|
|
18.
|
D
|
|
19.
|
B
|
|
20.
|
C
|
|
21.
|
A
|
|
22.
|
B
|
|
23.
|
D
|
|
24.
|
B
|
|
25.
|
A
|
|
26.
|
E
|
|
27.
|
C
|
|
28.
|
D
|
|
29.
|
D
|
|
30.
|
B
|
|
31.
|
B
|
|
32.
|
E
|
|
33.
|
C
|
|
34.
|
D
|
|
35.
|
A
|
|
36.
|
B
|
|
37.
|
D
|
|
38.
|
C
|
|
39.
|
B
|